LEGO(TM)s to the Stars:

Active MesoStructures, Kinetic Cellular Automata, and Parallel Nanomachines for Space Applications

Presented at 1996 International Space Development Conference, New York City, May 1996

Published in The Assembler, Volume 4, Number 3 Third Quarter, 1996

Tihamer Toth-Fejel

Abstract

Primitive molecular nanotechnology (MNT) will contribute significantly to the human settlement of Space by creating flexible, human-scale active systems that can be actively reconfigured into a wide variety of useful shapes and artifacts. It appears that a very large number of identical primitive nanomachines, operating in parallel as an Active Meso-Structure (AMS), may not only meet the requirements for such a system, but might also be easier to design, build, and control than drexlerian assemblers. These systems attempt to combine the respective strengths of Von Neumann's kinetic model and cellular automata (CA). Examples such as Josh Hall's Utility Fog, Joseph Michael's Shape-Shifting Flexible Robotic System, Forrest Bishop's XY Active Cells, and Goel and Thompson's Movable Finite Automata are described and compared. The claim is made that machines can only be self-replicating if they are built using MNT. Finally, a non-self-replicating method of constructing these primitive nanoscale KCAs is described.

Introduction

An early vision of molecular nanotechnology has been the creation of flexible, human-scale active structures that are actively reconfigurable into a wide variety of useful shapes and artifacts. Such medium-sized structures could essentially replace clothes, furniture, appliances, utensils, and tools. In response to our commands and to changing environments, these Active MesoStructures would provide shelter, security, entertainment, and hundreds of other household and industrial services.

Eric Drexler detailed some of the possible applications of nanotechnology in Engines of Creation. Early on, people were frightened by the "gray goo" scenario, in which out-of-control replication and evolution of assemblers destroys every protein molecule on Earth. Later, it became obvious that it is difficult to design self-replicating drexlerian assemblers that feed on a disordered mix of undifferentiated molecules. This is partially because complex pattern recognition systems seem to be necessary to identify neighboring atoms and molecules out of disordered surroundings. Also, we do not have generalized algorithms or tools for unbinding undifferentiated molecular bonds. Finally, there are many problems in achieving material and informational closure when designing a robust process for self-replication. One way around these problems, and around the problem of the consequences of self-replicating nanomachines, would be to have large numbers of more limited nanomachines that couldn't make or break molecular bonds, that didn't operate in random and surroundings, but only interacted mechanically and electronically with each other in well-defined ways. Such a technology would not only be easier to build, but it would also be safer because it could not replicate and evolve. Unfortunately, because such a limited system could not replicate itself, it would not be "as cheap as dirt and sunshine", but latter we shall examine an avenue for keeping the cost from becoming prohibitively expensive.

Each individual nanomachine would be a robot similar in some ways to John Von Neumann kinetic model (the robot in a warehouse full its subcomponents) in that it would actively move in its physical surroundings. But it would also share many of the characteristics of his cellular automata (CA), in that the legal set of interactions between individual nanomachines would be limited. Such a compromise between his theoretically approachable CA (cellular automata) and his practical, but mathematically unwieldy, kinetic model might result in a workable solution. A popular instance of CA is exemplified by John Conboy's mathematical game of "Life", now a screen saver on many computers, and it gives an idea of what shapes are possible. In ordinary CA, the individual cells cannot move -- they can only change state -- and the pattern moves across the static array. However, some innovative designs allow individual cells (not just patterns) to move with respect to each other, allowing the physical system to change shape just like the virtual patterns do. Ultimately, such Kinematic Cellular Automata (KCA) would be implemented in the real world, and would therefore be subject to gravity, tensile strength limits, Newton's laws, friction, thermodynamics, and other manifestations of Murphy's law. Ideally, such massively parallel systems would actively respond to user requests, forming medium-sized structures such as chairs and houses, and medium-sized machines such as toasters, computers, and automobiles. When viewing such devices from the point of view of their many components, KCA (Kinematic Cellular Automata) is an appropriate term to use. However, from a point of view of the final object with which humans can interact in the real world, it makes more sense to emphasize the system, its size, and its changibility -- "Active MesoStructure" (AMS).

Utility Fog

Bothered one day by a chaffing seat belt, J. Storrs Hall imagined how nanotechnology would replace it, and he ended up inventing Utility Fog. He imagined a user-friendly, completely programmable collection of avrogadro numbers of nanomachines that could form every kind of transportation, from horses to spaceships. It could simulate any material from gas, liquid, and solid, and it could implement the ultimate in virtual reality. Finally more speculative projections envision uploading human minds into planet-sized collections of Utility Fog. Before dismissing such speculations too quickly, it may be worthwhile to examine it closely for useful concepts that may be applied in the near term.

Hall provided an important baseline examination of the issues involved in the application and design of Utility Fog. Footnote1 He envisioned Utility Fog as an active polymorphic material designed as a conglomeration of 100-micron robotic cells, or foglets, built using molecular nanotechnology. An appropriate mass of Utility Fog could be programmed to simulate, to the same precision as measured by human senses, most of the physical properties, such as hardness, temperature, light, of any macroscopic object, including expected objects such as tables and fans, but also materials such as air and water. The major exceptions would be taste, smell, and transparency. To users, it would seem like the Star Trek Holodeck except that it would use atoms instead of holographic illusions.

Utility Fog could operate in two modes -- "native", and "fog". In "naive" mode, individual foglets would move into different positions and perform certain mechanical operations depending on what object it was forming. For example, if it was formed to be part of a table, then it would be motionless and locked. If the object was a fan, then most of the structure would remain locked, and only the foglets between the two parts would need to move. If the object was a galloping mechanical horse, then significant numbers of foglets would need to move around in a coordinated fashion, in response to user commands and environmental conditions. The saddle might use accelerometers or pressure sensors to actively cushion the shock for the rider, and might provide electric heating or microfan cooling to adjust the temperature. With a suit made of Fog, you might wrestle alligators, cheating a little by having the suit amplify your movements as it protects you from the alligator's teeth.

In "fog" mode, the foglets would not move, but act more like pixels on a television screen -- they would "pixelate". The foglets would vary other properties according to which part of the object they are representing, generally transmitting information and sound. A Fog-filled room would contain 90% air, and surround its occupant with a display screen with 100 micron resolution. Meanwhile, each liter of foglets behind the display would contain about a billion times the processing power of a 286 PC, making possible some pretty impressive virtual reality simulations. Mixing the modes would allow you to ride a "native" burro down a "fog" Grand Canyon (feeling every bump along the hot, sun-beaten path), or wrestle "native" alligators in "native" liquid in the "fog" Everglades, or fly a "native" airplane into a real thunderstorm at night and make it seem to the pilot like riding a "fog" Pegasus into that same thunderstorm during the day.

Foglets

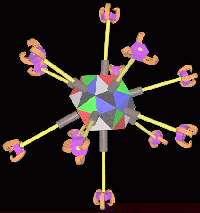
Figure 1. Foglet

Compared to a drexlerian assembler, foglets would be huge (100 microns), overpowered, and imprecise -- able to control their motions to about a tenth of a micron (one micron equals a millionth of a meter) instead of a tenth of a nanometer. The other main difference is that foglets won't control chemical reactions via mechanosynthesis, as dexlerian assemblers will. Each foglet consists of a central body with twelve telescoping and swiveling arms arranged as the faces of a dodecahedron

Each arm has a three-fingered locking gripper at its end, providing four degrees of freedom and a relatively rigid mechanical connection along with a precise optical and electrical interface for information and power transfer. Foglets run on electricity, and by telescoping their arms, could vary their density from less than cork to ivory. Presumably, the foglet body would be covered with red/green/blue LED film that would be activated while in "fog" mode.

Fog Limitations

By examining many of the engineering details in his design, Hall has found many interesting limitations to Utility Fog, and some work-arounds. He found that a pure diamond structure should not be employed, even though it would result in the maximum tensile strength of the components. This is because the very high surface area of carbon would make the Fog a fuel-air explosive. The solution is to build much of the foglet's structural exoskeleton out of aluminum oxide or quartz.

In "native" mode, things just can't appear out of thin air. It takes time to form objects. Since the foglet arms can extend and retract at rates of ten meters per second, a single sheet of foglets can move no faster than that. On the other hand, there is no reason for foglets to only move one sheet at a time, so formation times for objects can still be quite fast.

Another problem results because the arms extension and retraction rates do allow Fog to move at 100 meters per second (220 miles per hour) for each millimeter of thickness. This capability would only be possible if the motions of each individual arm generated almost no heat -- otherwise you would have another explosion on your hands (well, a meltdown, anyway). The solution is to use the movement of arms as generators as well as actuators, storing the excess mechanical energy in hydrogen gas buffers.

Packed Fog would only be as about strong as aluminum, and in that packed mode (with arms completely retracted), would not be dynamically polymorphic. In other words, even at it's strongest, it wouldn't make a very good knife, and it couldn't move without expanding first.

Since Fog would not interact at a molecular level, it could not chemically alter materials as in creating food. Eating Fog would be like eating sawdust. However, Fog could mediate chemical processes, like cooking, the same way a breadmaker does -- by mixing, stirring, and heating.

The components of the foglets themselves -- motors, computers, and communications, are all within the limits of conservative engineering principles. However, there are a number of scientific unknowns regarding many of the Fog claims, not to mention considerable engineering work. Ironically, the most difficult part of Fog is something we do pretty well now: software. It is not clear, for example, whether each foglet should be individually addressable. Also, the reliability issues of individual foglets, and of the entire system, have not been examined. Current computer networks can handle most cases of malfunctioning computers, but not all of them, and certainly no protocol can handle avrogadro numbers of nodes on a network. Physical removal of broken foglets is also difficult -- one can imagine a section of Fog getting progressively worse as pieces of broken foglets interlodge between the arms of working foglets, reducing performance, creating waste heat, and damaging more foglets. Finally, engineers will need to solve the little-understood problem of how to recognize when a distributed control system goes out of control, and what do about it.

One of the major problems with fog is that foglets are so complicated. Construction of a two dimensional fog-like system with more limited functionality would be much simpler than for regular Fog, and for economic reasons may provide an important pathway to true Fog. The dynamics of flow, including foglet positional detection and control, path planning, and gripper reconnection when arms and foglets are moving relative to each other are computationally daunting, so a simple two-dimensional Utility Film would never detach from its neighbors. Such a layer of filmlets could form an active membrane that could expand and contract, grind, wave, or sift while in "native" mode, or, while in "fog" mode, act very much like regular fog, pixelating input and outputting information. The applications would still be impressive: wall-sized television and computer displays with a 40,000 DPI resolution (including screensavers for decoration and sunlit scenes to provide room lighting), adjustable active membranes for actively filtering particulate industrial waste, engineless transportation surfaces, and surgical equipment).

Joseph Michael's Shape-Changing Robots

While Hall's foglets closely resemble TinkerToys(TM), another, more conservative KCA (kinematic cellular automata) is more similar to LEGO(TM) blocks. Joseph Michael envisions flexible robots that can flow through small openings as they work on a wide variety of tasks. Like Utility Fog, Michael's concept also involves at large numbers of individual machines, but instead of dodecahedral foglets with telescoping and swiveling arms, his paradigm is a simpler one consisting of solid bricks or cubes with retractable wedges. Michael has not only patented his flexible robot, but he has also built and tested models, and demonstrated them at trade shows. Footnote2

Michael defines his shape changing robot as "a finite resolution electromechanical device that acquires dynamically programmed geometric shapes though the use of computers to within the limits of the resolution imposed by the electromechanical mechanism and/or the software running on the computers". Figure 2 shows a docking between two shape changing robot satellites. To operate this mechanism, the top system extends a capture rod through the ring. Then the bottom system contracts the ring to ensure a solid contact between the two vehicles.

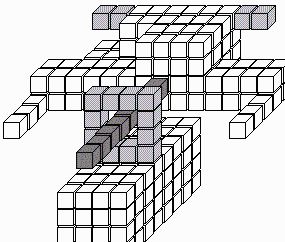
Figure 2. Two Shape Changing Robots

On land, the robotic systems would change shape by extending streamers made up of individual cubes onto which they transports themselves. Many streamers could be erected simultaneously, allowing rapid transportation of material (The Assembler published an early version of Michael's article last year, so we won't go into too much detail here).

Cube Description

Each computer controlled cube is identical to its neighbors, and contains sensors and electromechanical devices. It can move in the x, y, and z directions, receive and act in response to external instructions or sensor data, lock any of its faces to any of its six neighbors, receive and transmit power at any of the six faces, and communicate with any of its neighboring cubes via a standard network protocol.

There should be a minimum of one master computer issuing control messages to robotic cubes. The remaining robotic cubes should be slaves, receiving and executing instructions received through the networking ports.

Ideally, the instructions from the master computer would be at a high level, with submaster cubes calculating (in parallel) the lower level sub-instructions at a local level. Ideally, the master computer should be just another cube, so that in case of failure, another cube could take over. Each active cube should have, if not a full computer, at least a minimal controller that obeys instructions directed to it. It would not do any further computations other than send back acknowledgments and sensor overloads. Such a minimal controller would probably have about 1K RAM and 10K ROM.

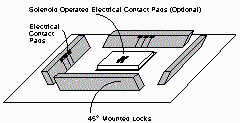
Figure 3. Cube Face (wedges extended)

The mechanisms of movement are straightforward, as seen in Figures 3 and 4. One part of the mechanism consists of four 45 degree wedges that push out under computer control from each face. The wedges insert into complementary slots in the opposing face of another cube. When fully inserted, these wedges maintain a separation gap between the cubes, so that when the cubes slide, friction is minimized. Michael has tested wooden models and found them to be extremely strong when locked.

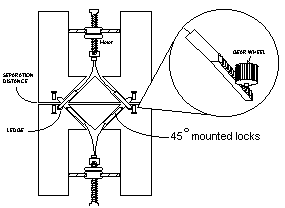
Figure 4. Wedge Mechanisms

The wedges are serrated, so that when pushed into an opposing slot, they are engaged by a gear wheel (effectively forming a rack and pinion) that can be driven by the opposing cube. The point about doing it this way is that the moved cube (the one with the wedges sticking out) is not powered up when it is moved. There are no sliding electrical contacts to wear out, and in the unusual circumstance of moving a powered cube, specialized cubes connected by an umbilical cord would be used as the interface between the powered cube and the rest of the system if that was the only power source. Most systems could have more than one power source, so that there is always power, even when one power pack is switched off in order to be transported around the structure.

Limitations of Michaels Shape-Changing Robot

Movement is only in the X, Y, and Z directions, and angular directions cannot be achieved, though for most applications, shape-changing could approximate it closely. For example, ordinary cubes could form a bucket, and while the contents could not be tipped out, the bottom could move aside, emptying the contents.

As with foglets, there are a number of unanswered questions to Michael's cubes: Because of Murphy's law, connections and mechanical devices eventually fail. What specific algorithm would individual cubes use to detect open and closed electrical circuits? How would a shape-changing robot decide that one of its cubes were defective in some way, and how would it get rid of it? How will the cubes deal with the dirt and mud prevalent in the real world?

Similar to foglets, software may also prove to be a serious roadblock, since some physical and computational tasks are easy to parallelize, while others are not. If they are not, then the master computer slows down from the sheer number of calculations, and the system is further slowed down by the bandwidth of the cubes, limiting the number of cubes that can move at any one time. Michael is currently working on a fractal operating system to address some of those issues.

Bishop's XY Active Cell Aggregate

Last quarter's issue of The Assembler described an interstellar explorer application designed from KCA developed by Forrest Bishop. His robotic "Shape Shifter" is an aggregation of similar, space-filling polyhedral machines, each capable of moving with respect to its adjoining neighbors, singly and in groups. While Michael has a practical, inventor's bent on KCA cells, Bishop's major contribution is of a more theoretical bent. He quickly realized that since the cubes would never rotate, the interfacing didn't have to be universal. Second, he differentiated between surfaces that slide parallel to each other, and surfaces that separate by simply pulling apart. In doing so, he was able to define a simplified XY cell that was a subset of an XYZ cell. Finally, he was able to categorize all the trajectories of a two-dimensional five-cube configuration, an important step in designing the control software. Footnote3

Movable Finite Automata

The artificial life conferences have generally concentrated on cellular automata and robotics, but Narendara Goel and Richard Thompson have devised a KCA-like hybrid in the search of building better models for understanding biological systems. Footnote4 They explored four models for self-organization in living systems:

1. Analogous models such as L-systems,

2. Physically realistic models, ultimately (and computationally ridiculously) attempting to solve Schrodinger's equation,

3. Reaction-Diffusion-Equation based models that represent various chemicals in three-dimensional space but don't represent the three-dimensional configuration of the individual molecules, and

4. CA models that lack physical realism but are readily analyzable and simulatable.

Out of these four, they developed a new class, best described as a hybrid between CA and biophysical models. These Movable Finite Automata (MFA) are finite state automata that undergo discrete changes in a step-by-step fashion, allowing them to move and interact with each other to achieve greater biophysical realism. They simulated this model (rather easily, since each cell is a finite state machine) to analyze the T4 bacteriophage, and were able to simulate T4 construction and behavior. Detailed experimentation showed that there were three important principles of self-assembly:

1. Subassembly -- subunits must be assembled in stages. For example, a unit consisting of 1000 subunits should proceed by assembling ten subunits into an intermediate grouping, and then ten of these into a bigger intermediate group. This is what happens in the industrial world, presumably for the same reasons: efficiency (parallel operations), reliability (bad intermediate groups can be discarded), and variety (one bolt can be used in many mechanisms).

2. Minimization of Free Energy -- The thermodynamics must drive the arrangement and keep it from backing up.

3. Sequential Assembly and Conformational Switching --

The shape of the subunits naturally permits only one series of steps for assembly.

Comparing and Contrasting KCAs

All KCAs face similar design challenges, especially in mass manufacturing and software control.

Unlike foglets, cubes cannot change their density by extending or retracting telescoping arms. For the same reason, they are denser and stronger. Also, the simplified design of cubes makes it impossible for the AMS which they comprise to rotate on an axis. On the other hand, this same simplified design makes it much easier to build cubes than foglets, making it more of a near-term engineering reality. Cubes won't have to worry, as foglets must, about sharing a precise coordinate system with neighbors, or kinematically sensing twelve arm positions, or visually sensing objects that these arms may destructively or unexpectedly encounter.

Hall envisioned his foglets at a molecular level, and realized that the design would work even if the foglets were a thousand times bigger. Michael started from the macro world of flexible robots, and realized that they could be made at nanoscales.

Personally, I consider Hall foglets the DeLorean of KCA -- a great design, but too far ahead of its time. Michael and Bishop cubes, on the other hand, I consider the DOS of KCA - I hate some if their limitations, but its the one to bet on.

Parallel Machines

Currently, most machines are built out of many different parts. The classical robot, for example, consists of thousands of mechanical and electrical parts, and only a few of those are the same. In an assembly line, identical parts are manufactured that can be interchanged between the products in which the parts end up. DFM (Design For Manufacturability) tries to improve on that practice by reducing the parts count and part types count. Parallel machines simply take these concepts to the logical extreme -- they are composed of mostly identical parts. An abacus, a memory chip, a massively parallel computer, a geodesic structure, a molecular sieve, and a railroad track are some examples. Many children toys such as Lincoln Logs(TM)), Erector Sets(TM), and LEGOs(TM) are also minimal parts type examples. Note that there is a Tinker Toy(TM) mechanism at MIT that can play Tic-Tac-Toe, so even the simplest units can exhibit very complex behavior when configured properly.

It does not matter if the basic unit part is primitive. Muscle cells can only contract; they have 1/2 degree of motion, but collectively they power the human hand, which is still beyond any existing human-made machine's capability. Given the goal of a parallel machine that can actively shape itself into arbitrary three dimensional forms, what are the minimal requirements for a basic unit? Are there any other capabilities we can get for no additional cost?

Any useful AMS is going to require thousands, if not trillions, of the basic unit. This cost would greatly exceed building with normal multi-part methods. But one has to remember the economies of mass production. Designing and building the first basic units would be expensive. But once they were in mass production the cost would plummet down to the milicent level. Just like the ICs that individually would cost more than the entire computer they are a part of, the more one builds, the cheaper they are to produce. Since there would only be one kind of basic unit that could be used to build numerous different kinds of things, we would be manufacturing more of them than any part made today.

Programming such a massively parallel machine is not easy. However, software and hardware technologies have made advances that promise to harness computer power to solve problems by using many inexpensive processors instead of one extremely powerful (and expensive) processor. Three avenues have been explored: SMP (Symmetric MultiProcessors), MMP (Massively Parallel Processors), and NOW (Networks of Workstations). SMPs have enjoyed some commercial success, but they have severe scaling problems. While MMPs and NOWs have problems, it appears that a well-designed hybrid of the two would eliminate the deficiencies of both. This hybrid, known as LAMP (Local Area MultiProcessor) shares a more intimate connection than a LAN, with shared memory and very efficient message passing. A LAMP implementation must possess a number of important properties:, including salability, a standardized interface, minimum latency , coherence, atomic operations, synchronization, starvation and deadlock avoidance, interconnect independence, generalized I/O and processors, and broadcast and multicast features.

One of the promising implementations of LAMP is ANSI/IEEE Standard 1596 Scaleable Coherent Interface Footnote5. There are rumors that Silicon Graphics is working on a prototype.

Research in Artificial Life has shown that complex behavior can be generated relatively easily, though sometimes the results are unexpected. Many interesting shapes have been generated in CA arrays and related systems. In addition to Conway's Life, one of the best research areas are known as L-systems, or Lindenmayer systems Footnote6 which have "grown" very realistic looking biological structures such as plants and more efficient biological imitations (such as neural networks Footnote7) from simple mathematical algorithms. L-systems are a mathematical construct that can be viewed as a special class of fractals, and are based on a parallel string rewriting mechanism. The resulting strings, after repeatedly applying production rules on an initial axiom, can be interpreted in such a way that the results are line drawings that look like trees. Turtle graphics are a popular implementation of L-systems, in which only four commands and a stack are necessary for very complex results.

The advantages of L-systems fit in well with massively parallel systems:

1. Sparse coding: Very few rules can produce very complex behaviors and shapes.

2. Salability: Arbitrarily large architectures can easily develop from small ones.

3. Modularity: The same production rules can be applied many times in the growth process, resulting in multiple application of efficient subsystems.

4. As a blind imitation of biology, L-systems provide some unknown design principles.

Another way of thinking about parallelizing behavior in cells involves a broadcast approach. These schemes are useful if the assemblers can blindly follow linear instructions, and would work for large numbers of cells floating in a vat of an appropriate liquid. The mode of broadcast could be varied -- they may consist of chemical chains which would be dumped into the vat of assemblers, or as Drexler has suggested, acoustic signals at some reasonable data rate (a megabit per second is technically unchallenging and should suffice). Footnote8

For example, the following process could be followed: Designate a single cell, called the "seed," to have the coordinates 0,0,0. Any cell that comes into contact with the seed is given coordinates from the seed based on its location with respect to the seed. Note that it is not even necessary to determine a global coordinate system, for the cell orientation will determine the final global orientation. However, the seed could obtain its orientation from the boundaries of the system. A simplifying assumptions would be that each cell is mechanically constructed as a cube, so that it can bind to six adjacent cells that are located on the faces of a cube centered around it. It can transmit information to or receive information from these cells. When two arbitrary cells connect, they can either remain connected or disconnect again. Normally, when they are in solution, two cells will disconnect. If, however, an cell connects to the seed, it will remain connected, and obtain its coordinates from its new neighbor. These coordinates will let the newly joined cell determine its distance from the seed. Cells that are farther from the seed than this distance will then disconnect, while those that are closer than this distance will remain connected. Thus the growth of the cluster of cells will be limited as most of the cluster is filled in before the size of the cluster is increased. Periodically, the current diameter is increased and broadcast to all the cells. Note that a variety of distance metrics are feasible, so the resulting "sphere" of cells can be any of a variety of shapes.

This algorithm will permit the growth of a cluster of cells, and will assign coordinates to each cell. Broadcast transmissions can then address individual cells or arbitrary groups of cells. The obvious limitations of this algorithm are growth rate (each layer, one cell thick or on the order of one micron thick, will take some fixed period of time to grow) and the handling of errors.

The most pernicious errors are caused by erroneous coordinates that are spread throughout the cluster. Local voting algorithms, however, can reduce the probability of this sort of failure to an acceptable level. A simple voting algorithm would have each cell adopt as its own coordinate the coordinate agreed to by a majority of the cells in the vicinity. An cell in disagreement with those in its vicinity would be isolated.

Once a sufficiently large cluster has been formed, the broadcast information can be used to specify which groups of cells are to build what substructures. As each cell knows its own coordinates, it could listen to the appropriate part of the broadcast and ignore the rest. (Anyone familiar with the SIMD (Single Instruction Multiple Data) architecture will recognize the approach). Provided that the structural complexity of the object is not excessive, the relatively slow broadcast information will be sufficient to describe it. At a megabit per second, 3.6 gigabits of data can be broadcast in an hour, so the structure would have to be very complex before this approach would fail.

If the growth rate of the cluster is too slow, multi-cluster algorithms which grow several clusters simultaneously can be adopted. Such algorithms would then have to merge clusters, just as the algorithm described was able to merge individual cells. Hierarchical algorithms that merge clusters of clusters, clusters of clusters of clusters, and so forth are feasible and should improve growth rates. Footnote9

The mega-clustering approach leads to a third way of thinking about parallel programming, convergent assembly. Such a hierarchical view is analogous to the software technique of using subroutines to handle subtasks. It is also analogous to the traditional view of an organization. The idea is to use local, semi-autonomous control (a clock is necessary for coordination purposes) to assemble small components using small positional devices, and in their turn are assembled into larger components by larger positional devices. Such a series of steps allows the construction of large systems with very high precision without the necessity of directly coordinating large numbers of autonomous cells.

All the above approaches to controlling massively parallel systems depend on deterministic, completely controllable systems. Agoric systems (see Drexler) are one example that go against this mode. Distributed building is another, for which a formal model was inspired by the observation of wasp colonies. Algorithms have been obtained that allow a swarm of simple agents, moving randomly on a three-dimensional cubic lattice, to build coherent structures.

Individual insects generally possess a limited behavioral repertoire, but social insects are collectively capable of performing complex tasks, such as nest building, through the direct or indirect interactions taking place between individuals. In many cases, the structuration of the environment caused by the colony's activities structures in turn individual behaviors, in a process that Grasse' coined stigmergy. He showed that task coordination and regulation of the building activity in termites do not depend on inter-actions between the workers themselves but are mainly achieved by the nest structure: Individual behaviors are controlled and guided by previous work. Every time a worker takes a building action, it modifies the local configuration that triggered its building action. The new configuration then automatically stimulates new actions from any worker in the colony. Footnote10

MNT vs. KCA

KCA cells would be easier to design and control than drexlerian assemblers because each KCA cell has a very restricted set of capabilities, while an assembler could recognize and manipulate any atom, in addition to making or breaking any chemical bond between any two or more atoms. Even if only a limited subset of this desired mechanochemosynthesis capability is achieved, the enormous number of possibilities are overwhelming to the control system, and the human programmer designing it. In contrast, KCA capabilities are much simpler. Therefore KCA are much easier to understand, design, and control.

The restricted capabilities of KCA form a useful intermediate layer between molecular manufacturing and macroscopic applications. KCA are more energy efficient in reshaping macroscopic structures than drexlerian assemblers because they move cells and information, and they don't form or break chemical bonds. They are also more computationally efficient than reshaping objects at the molecular level because they move atoms in cell size or multi-cell size chunks, rather than explicitly specifying the position of every atom. They have lower design costs than molecular manufacturing, though at reduced capabilities for the final product (e.g. tensile strength). KCA relates to molecular manufacturing as a field programmable gate array relates to a custom integrated circuit, or as an interpreter relates to a compiler. They all cut design costs at the cost of reducing some other desirable characteristic of the product.

KCA and Self-Replication

As far as MMSG is concerned, the goal is to build self-replicating lunar and extraterrestrial factories for developing Space for humanity. One implementation is described in the 1980 NASA/ Santa Clara Summer study. KCA is not designed to self-replicate, but an analysis of how it would need to be expanded to include that capability is instructive. Even in an environment full of large subcomponents, Michael's cells are about as useful as bulldozers, though a set of fractal cubes decreasing in size could build all but the smallest cubes. But then how are the smallest cubes built?

I believe that making KCAs self-replicate in the wild is impossible without MNT. While I was working on my master's thesis, Self-Test: From Simple Circuits to Self-replicating Automata, I found that an essential ingredient of self-testing is the hallmark of the "conquer and divide" strategy used by engineers and technicians everywhere -- before you can test an entire system, you must test its subcomponents. And the subcomponent's sub-sub-components, etc. How does one test, clean, and repair a macro-scale refining complex? In the course of writing my thesis, I found myself doing chemistry instead of electrical engineering (which is what my master's was in), so I gave up temporarily and turned to the comfortable world of self-replicating and self-modifying software. At the Houston ISDC, I complained to Eric Drexler about my problem. In his characteristic dry wit, he said, "God has pretty good quality control on atoms." The point is, mountains, rivers, and planets don't process information, metabolize matter and energy, maintain homeostasis, and self-replicate, because they can't adequately test, repair, and otherwise manipulate their smallest subcomponents. Carbon-based lifeforms from Earth can do all those things because they test and repair themselves down to the ultimate subcomponent level -- atoms. Present day factories seem to replicate, as do the robots building other robots in Japan because they are tended by atomically precise mechanisms -- humans.

On the other hand, John Von Neumann also did some work on probability automata -- i.e. robots with components that would fail occasionally. So it might actually be possible to build a macro-based self-rep system in the disordered world. But I suspect that it would be a lot more complicated than a nanoscale system.

Integrated Circuits have a concept of "scaleable device pairs" in which the imprecise masking process may make the capacitor twice as large, but there is a compensating inductor whose value (because of the configuration, geometry, and the physical dependencies) automatically becomes half as large, so the total impedance remains the same. I am uncomfortable with this concept because it means that the parts are not interchangeable, though the micromechanical people are trying to implement such a scheme. I think it will work for them because the parts that operate with each other are manufactured together. But in essence, that is really a type of craftsmanship, not manufacturing. My point is that when you start making relatively small things such as in microtech, then an extra layer of atoms can make a big difference, and these differences keep the parts from being interchangeable. The opposite tack, of achieving self-replication making the parts really big, sounds nice because then they're easier to work with, but the problem is that you're going to need about a billion subcomponents (Von Neumann's estimate). A billion of any macro object, even at 2 cents a pound, is expensive. Plus really heavy things have to start worrying about gravity effects, just as really small things have to worry about static cling and surface tension (Editor's note: Next month's issue will contain a lot of counter-arguments by Frietas and Francis on this section).

Construction

But what about actually building KCA? To build trillions of them, isn't self-replication necessary? Even at a penny each, a thimbleful of 100 micron cells would cost $1013! On the other hand, electronic switches (tubes) at one time cost a few dollars each, but you can now buy 1 MB RAMs for $50, or four thousandths of a cent per electronic switch (transistor). Unfortunately, even at that price, KCA is pretty expensive for almost all applications. However, harvesting the results of three stages of bootstrapping, none of which involve universal assemblers, may lower the cost enough for commercial viability.

The approach is to work the problem backwards in the form of a simplified needs analysis: Envision a membrane with raw materials on one side and a solid mass of KCA cells pouring out the other side. The problem reduces to designing the membrane that does this assembly process. This membrane is an array of single-purpose nanomachines -- they make only KCA cells. This array would in turn be manufactured one line at a time by a long filament of connected, single-purpose nanomachines. And each of these is in turn manufactured by a third type of single-purpose machine. Let's take a look at the process in more detail, in the actual order of manufacture.

We would start with a single master nanomachine, called a MasterMaker(MM), which would need to be built by any means possible (almost by hand, at first, but at the IBM rate of 7 atoms/hour, it could really use some pre-assembled parts, such as Merkle bearings made by bioengineered self-assembly, etched nanolithography, bulk chemistry, or some combination). MasterMakers could only do one thing: out of a supply of atomically precise raw materials, build a repetitive string of connected, limited capability, nanomachines -- an assembly line. Practically, you would need a number of these MasterMakers working in parallel, each building assembly lines, called NanoLines (NL), which you would then connect into a meter-long filament, using a small number of special-purpose LineConnecters (LC), whose only ability lies in identifying, manipulating, and connecting segments of NanoLine (NL). These LineConnectors (LC) would also need to be made by hand from pre-assembled parts, the same way MasterMakers would be.

*MM*-NL-NL-NL-NL-NL-NL

MM*-NL-NL-NL-NL-NL-NL

Figure 7. Three MasterMakers (MM) are generating three NanoLine(NL) filaments toward the right (raw component feed not shown).

NL-NL-NL-NL-NL-NL==LC==NL-NL-NL-NL-NL-NL

Figure 8. A LineConnector (LC) is connecting two NanoLines (NL) segments (raw component feed not shown).

A NanoLine (NL) would be a filament of connected nanomachines, a one-dimensional hybrid between MasterMaker (MM) and AMS cell. A NanoLine could do only one thing -- assemble atomically precise raw materials into a third type of nanomachine, a GenGrid (GG).

NL-NL-NL-NL-NL-NL-NL-NL-NL-NL-NL-NL-NL

|| || || || || || || || || || || || ||