Presents four models for siting an orbiting manufacturing facility with respect to two inputs and one market location, each progressively adding cost elements. Addresses space transportation using molecular nanotechnology, with a focus on solar sails and rotating tethers. Addresses space manufacturing with a focus on the particular strengths of molecular manufacturing and space manufacturing. Identifies two system concepts for using molecular manufacturing in space. Identifies open issues, and urges further work in the area.
Preliminary examinations suggest individual molecular nanotechnology-based space systems should be capable of dramatic performance5,6,7,8, but McKendree9 also notes that these individual performances are so high as to probably qualitatively transform their context and environment, complicating analysis of the real utility of these capabilities.
Location theory10 offers one way out of this problem, by raising the analysis to the level of integrated super-systems of manufacturing facilities and transportation systems. Thus, a reasonable next step towards understanding the implications of molecular nanotechnology for our future space operations is to achieve the following four-part program:
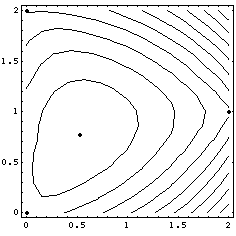
The function creates a single continuous basin on the plane, and is easily solved both by geometric and by simple optimization approaches.
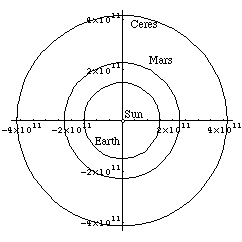
This topic will be illustrated with a recurring example, where the input locations are taken to be circular orbits roughly corresponding to the orbits of Earth and Ceres, with the market location a circular orbit roughly corresponding to the orbit of Mars.
The difference between the four two-input models presented below is the different cost functions used. Each adds a new feature to the transit cost model.
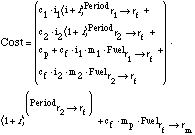
V) for a Hohmann transfer orbit. Since the equation
is11:
(1)
This can be expressed as:
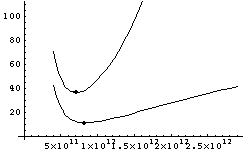(2)
Where r1 is the orbital radius of the first input, r2 is the orbital radius of
the second input, rm is the orbital radius of the market, i1 is the ratio of
mass of input 1 needed for each kg of the product, i2 is the ratio of mass of
input 2 needed for each kg of the product, ct1 is the cost to transport 1 kg of
input a V of 1 m/s from the location input 1, ct2 is the cost to
transport 1 kg of input a V of 1 m/s from the location input 2, and
ctp is the cost to transport 1 kg of product a V of 1 m/s from the
market.
[Note, in a more sophisticated model the cost of fuel at the facility could vary with rf.]
The simple case, where all the input ratios and transit costs are 1, is shown in figure 3 above.
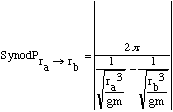
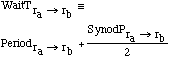(3)The new variable is v0, which is the ideal exhaust velocity, or specific impulse times g. The cost function is parallel with (2).
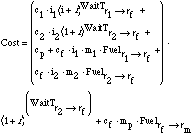(4)
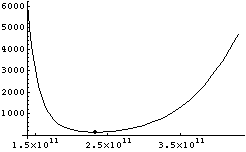
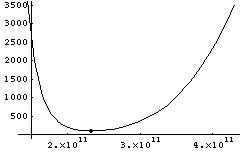
A v0 of 4410 m/s, yields the cost curve in Figure 4. Note that
unlike total V, fuel usage has a continuous derivative. Direct
optimization is simple for this model.
The carrying cost for inventory in orbit is the interest charge on the price of the inventory (either an input or a product) over the transit time.
The period of transit for a Hohmann trajectory can be calculated as:
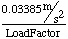(5)This gives a cost function of:
(6)The key new variable, i, is the interest rate. The variable cp is the cost of producing the output out of the inputs. In previous models it did not matter, since it is treated as a constant, independent of facility location. For different transit times it will be subject to different interest charges, however, and thus must be explicit in this model.
Remember the ideal exhaust velocity, v0, is buried within Fuelra->rb.
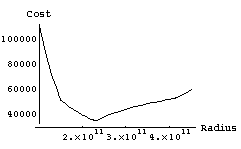
An interest rate of 20% per year is sufficient to force a tiny adjustment in the optimal facility orbital radius on our basic example, and yields the following cost curve:
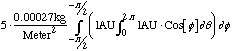
In this case, interest charges on material are dominated by the mass ratio costs. To better illustrate the effect of inventory carrying costs, consider a second problem with longer transit times. For example, Lewis12 suggests mining He3 from Uranus. Let the inputs coming from circular orbits at the radius of Ceres and Uranus, and the market in a circular orbit at the radius of Jupiter (maybe a Trojan asteroid). To keep the graph readable, i has been reduced to 10%, appropriate for a conservative operation. Keeping all the other numbers the same yields the higher of the following curves.
,
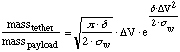(7)
rb
when ra =
rb.]The waiting time is intended to represent the time that must be spent between the purchase of an object at a base, and when it can be delivered to another base via a Hohmann trajectory. It is defined here as the period of the Hohmann transit, plus one-half the synodic period.
(8)Interest charges on inventory in waiting time will capture the economic cost as extracted resources wait for shipment and delivery to the facility, and as finished products wait for shipment and delivery to their market (end user). Incorporating this full waiting time into the model yields the cost function:
(9)
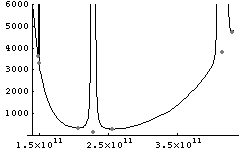
WaitTra->rb is no longer continuous, however, and indeed goes to as ra
approaches rb. This drives the carrying costs to (given any positive
interest rate), and thus creates a discontinuous cost function, as shown
below:
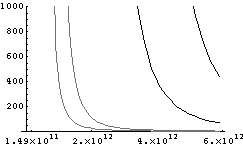
These discontinuities are an artifact of the restriction to Hohmann transfers between orbits. Less energy-optimal trajectories would allow launches without waiting so long, and dramatically lower total costs for the very close orbits, which have long synodic periods. It is expected that this corrected cost function could be continuous.
Furthermore, molecular manufacturing (MM) can be used to re-form materials into new products, thus potentially turning the remaining parasitic mass into useful payload.
Drexler7,13 discusses MNT-based, solar-electric ion engines. By combining very low-mass, high-specific energy solar panels with arrays of very small ion engines, exhaust velocities of 250 - 1000 km/s with accelerations of 0.8 - 9.8 m/s2 should be feasible. When not thrusting, the large area, low-mass structure would be capable of limited solar sailing.
The solar sail's force is proportional to the solar flux, which is proportional to 1/r2 (where r is the radius to the Sun). The force due to solar gravity is also proportional to 1/r2. Thus, the ratio of the solar sail force to the gravitational force is independent of the distance from the Sun.
The solar constant is defined as the solar flux at 1 AU, 1370 W/m2. Dividing by the speed of light gives a solar pressure of 4.57 x 10-6 kg/(m.s2). This is the pressure from a one directional flux--bouncing light in the exact opposite direction doubles this pressure.
A 100 nm thick aluminum solar sail masses 0.27 g/m2, so the maximum acceleration due to light pressure is
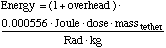(10)where the LoadFactor is the ratio of the vehicle's total mass to its solar-sail mass.
For comparison, the acceleration at 1 AU due to solar gravity is 0.005878 m/s2, less than a fifth of the acceleration from the force of light pressure.
By angling the solar sail, the acceleration due to the light pressure, and thus the total acceleration vector, can be varied.
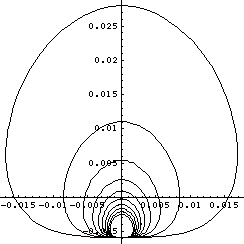
The feasible accelerations for a solar sail at 1 AU, with LoadFactors of 1 though 10, are shown in figure 8 below. At different solar distances, the magnitudes would change but the shape would be the same.
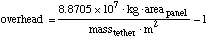
Even a load factor of 5 allows the solar sail to accelerate directly away from the Sun.
As a first approximation, the rate at which MNT could produce a solar sail would vary directly with the available power. At greater ranges from the sun, the solar flux would fall as 1/r2, however the characteristic orbital period would grow as r3/2 (Kepler's third law), so there still would be ample time to fabricate a solar sail and put it to effective use.
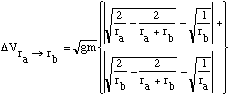= 3.8 x 1020 kg
(11)This may look like a lot, but it is only about one-fifth the mass of Ceres, while consuming the entire solar flux. If we consider only solar sails maneuvering within +/-3.5 degrees from the plane of the ecliptic, a zone which contains all the planets of Venus through Neptune, this allows only 2.3 x 1019 kg in transit at 1 AU, or 1.8 x 1020 kg at the radius of Ceres.
The actual budget for solar sail transit in the solar system is likely to be even lower, because there will be many competing uses for the solar flux. While the performance of MNT-based solar sails is impressive, there is not the solar capacity to support massive use of solar sails. Thus, most large bases should spend most of their time without solar sail aid. Furthermore, once significant use of the solar system's resources is underway, most bulk cargo should expect to travel similarly unaided.
This suggests a future need to coordinate such resources in the solar system as the solar flux. Decisions must be particularized to specific amounts in specific locations at specific times. One approach would be to create a central scheduling authority, responsible for allocating the solar resources, and scheduling their uses. A more flexible and open approach would be to define marketable rights to specific portions of the flux. The flux channels could then be bought, sold, rented, bundled, subleased, optioned, distributed (e.g., with mirrors) and otherwise allocated dynamically as conditions warranted. Note, a corresponding market in allowed "bads" (e.g., release of radiation, or reflecting of light where it is not wanted), might also be needed to fully coordinate the real effects.
Bishop discusses such an overall control function as part of his proposed system for interplanetary transportation8.
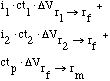(12)
where 
is the material density, 
w is the working (allowed) stress in
the tether material, and V is the change velocity when the tether
catches or throws, the payload. Thus, the tether can impart
2 x V, and
do so with the capture and release at different times and points on it's
orbit.
As McKendree9 discusses, one advantage molecular
nanotechnology offers to space systems is high strength to mass diamondoid
materials. With a of 3510 kg/m3, and a of 5 x
1010 Pa, a diamond tether could outperform those discussed by
Mackenzie15. Furthermore, his analysis required a safety factor of
3. With repair (see below), MNT materials should be able to maintain high
purity and low defects, allowing a more ambitious safety factor. Equation 12
is graphed below for diamond.
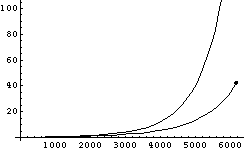
V (km/s), for diamond with safety factors of 2 and 3.With high mass ratios, tethers must serve many payloads to justify themselves. As to their performance, consider that the difference between the speed of Earth's orbit around the sun, and solar escape velocity, is a bit over 12 km/s. By providing half with a catch, and half with a throw, the tether indicated with the dot in figure 9 could pluck something from High Earth Orbit (HEO) and send it to any point in the outer solar system, including on a solar escape trajectory. The catch would require a challenging orbital rendezvous, however, since the tether would have to orbit the sun roughly 6 km/s faster than Earth at the point of capture. This does illustrate, however, that diamondoid tethers have significant potential for aiding transportation in the solar system.
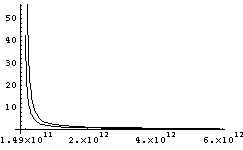
Indeed, since velocities fall as orbits move beyond the Sun, but the capabilities of rotating tethers stays constant, they are particularly attractive for transport in the outer solar system, Figure 10 illustrates the mass ratios for rotating tethers sized to operate in the region beyond Earth, both for safety factors of 2 and 3. Higher mass-ratio rotation tethers would be feasible, and more capable, particularly in dropping payloads into lower orbits.
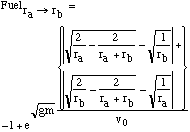
More aggressively, one could imagine a rotating tether in solar orbit, used to change the orbital plane 90deg.. This is ambitious, as plane changes are known to be very energetic and expensive maneuvers11. In one operational concept, such a tether would be in the plane of the ecliptic. Thus, vehicles in the main disk could dock with the tether at any time, and the tether would have to make the maneuver with a single throw. The mass ratio for such a tether in shown in figure 11, below.
To work, the tether must cancel the tangential velocity, and add an equal amount at 90deg.. This requires a throw angle of 135deg.. The angular momentum of the tether will stay pointed in a particular direct, however, and thus the tether will only be properly aligned twice per orbit.
One approach would be to use two counter-rotating tethers, physically coupled so they would have no net angular momentum, and could rotate through the orbit. A second approach would be to accept the twice per orbit performance, and place the tether in an orbit at a 90deg. inclination, with the disk of tether rotation in the orbital plane. This at least allows the tether to divide the maneuver into a capture and a throw. The mass ratios for this second approach are also shown in figure 11 below.
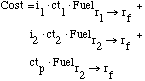
While such tethers appear to be in the realm of the feasible, the massive capital cost implied by the mass ratios, combined with their operational limits, suggests that alternate approaches might be more desirable. Gravity assists from Jupiter are effective. Nonetheless, these tethers offer a means over time to transform the solar system into a Dyson sphere.
(13)where "overhead" is the number of Joules required to locate and prepare to repair bonds, for each Joule spend in repairing the bonds. Note, this treats the repaired bond as endothermic, when actually it is exothermic. This is conservative, and provides a clear baseline for defining the probably much larger overhead.
A worst case could be taken to be 100 Rad delivered in 10 hours from a solar flare. Untreated, this would create a density of 1.4 x 10-7 failures in the structure to repair.
To power ongoing repairs, fast enough to keep up, even in this worst case, assume a 10% efficient solar panel attached near the pivot of the tether, and pointing towards the sun. Using the 1370 W/m2 at 1 AU, the allowable overhead is:
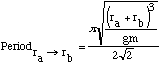(14)which suggests that repair should be quite feasible, but will also require ongoing repair at the molecular level.
Note, however, that MM must still pay the overhead of driving it's operating mechanisms, which will never run with thermodynamic perfection. Mill-style MM mechanisms apparently will be much more efficient than general purpose robotic devices. Thus, efficiency will be high for processing when all the material is already ordered within an MNT-framework. Energy efficiency will be significantly lower in the capture and initial processing of external material.
For space operations, this high energy efficiency is most useful for deep-space operations further from the sun, where available power levels will be lower. The high material efficiency offers most advantage to operations at locations in space where particular critical elements are scare, or must be shipped in.
This is significantly faster than the characteristic action time for interplanetary operations. Hohmann transfers take roughly half the year of the bodies transited between. Even the higher-speed possible with MNT propulsion (see above) gives characteristic interplanetary times closer to weeks than hours. Therefore, a reasonable approximation when at the early stages of stepwise refinement17 for a mixed MNT/interplanetary space system architecture, is to treat MNT actions as instantaneous compared to interstellar transits. Note, however, that this approximation should not apply without closer examination to the bootstrapped exploitation of in situ resources.
A major benefit of this flexibility in space operations would be greatly simplified logistics. Rather than waiting for parts, or stocking every conceivable part, MM could produce objects as the need arises. With a mission control providing support, fabrication instructions can be sent, and the space MM system need not even determine its operating instructions. Remember, however, that MM can only rearrange atoms, and when a chemical element is fully in local use, additional supplies would have to be supplied from elsewhere.
MM-based systems need not limit themselves to producing small products. They have the flexibility to encompass large assembly operations, producing almost arbitrarily large structures. For very large space systems, this could be quite useful.
Furthermore, building to atomic precision means building objects with very high quality. This can be important in providing long system life, and in allowing systems to safely operate with higher performance through lower safety factors.
Finally, atomic precision is required for molecular scale mechanisms.
As has been shown independent of MNT, bootstrapping offers tremendous leverage for space operations20,21,22, The natural ability of a mature MM to bootstrap provides the key strategic advantage for it's use in space operations.
The space environment includes a significant background radiation23, most of which we on Earth evade due to our planet's magnetic field and atmosphere. Strategies for dealing with this have included very heavy shielding24, but MM offers another approach--on board repair though dynamic remanufacture of subcomponents25, Preliminary calculations suggest that on-board repair through self-replacement of self-manufactured sub-components has the capability to dramatically extend system life. Key parameters are the support systems redundancy, the failure distribution shape, and the ratio of failure time to total repair time.
Similar to solar sails, MNT could also form a light pressure supported parabolic mirror, for concentration of large amounts of sunlight.
Furthermore, it is particularly promising that this vacuum is in the environment. Traditional MM designs are for systems that take external materials into themselves, and conduct the atomically-precise operations internally14,19. In space, the vacuum may allow atomically precise, highly reactive unit operations on the interface between the system and the environment. As "The greatest leverage in systems architecting is at the interfaces26," this is a very interesting possibility.
MM, however, does not require dumping noxious chemicals, as it can reform them5,28, and store unneeded elements for later use. For space operations, recycling is desirable, as there is a finite supply of desirable elements in the system. Thus, this advantage for space operations is not of tremendous use for MM.
Many intended space-manufacturing uses of microgravity, such as electrophoresis29, are intended to provide higher yields or quality by avoiding the distortions of gravity. Through convergent assembly from atomic precision, however, MM generally offers the capability to produce the same products, within Earth's gravity. This is because, at the local scale gravity is overwhelmed by the inter-atomic and inter-molecular forces MM exploits, and at the large scale deflections can be overcome by building atomically-precise proper sub-assemblies, and by assembling in a supported framework. Thus, MNT is a direct competitor to an orbital manufacture intent on exploiting micro-gravity in a process step.
Assembly in microgravity allows the construction of very large objects, including huge structures which could not support themselves on the surface under Earth's gravity. Roughly thousand km diameter rotating settlements6,8,30 and giant solar reflectors seem interesting.
Filtering and recycling impurities remains the final challenge. This requires MM tailored for each recycled input, and additional machinery to remove and store whatever else happens to exist. Fortunately, these stores can be examined, and additional cycles designed and added to remove those contaminants as well.
A potentially easier intermediate step would be to extend the model to ballistic non-Hohmann transits. This alone should eliminate the cost discontinuities from models with transit time.
The models shown restrict bases to locations within the same gravity well. Thus, the model works for bases orbiting the sun, and would work for bases in equatorial orbit around Earth, but does not consider bases in low orbit around different planets, nor consider bases on the surface of planets. This extension is critical, however, to support trade-offs between Earth launch of material, and in situ production.
Location theory itself focuses on single-product facilities. How can the it be extended to capture the utility of flexible facilities (such as a molecular manufacturing system)? Such an extension is probably best handled in stages.
The extension of discrete location theory to orbital space remains. Given the node-like nature of a set of orbiting objects, discrete models should prove more appropriate for many purposes.
While in-flight fabrication of solar sails using MM seems quite feasible, an actual process design needs to be sketched out. Furthermore, other solar sail designs have promise33, and should be investigated as architectures when using MNT.
The high performance of MNT-based solar sails suggests that other transportation systems based on reflecting solar light, such as solar flux distribution mirrors, are worth investigation with MNT parameters.
While basic estimates of MNT-based solar-electric ion engines are available7,13, more detailed examinations need to be published.
While on-board repair of radiation damage using MM seems quite feasible, especially since most repair can occur in the lulls between high-radiation events, a more detailed system design would be encouraging.
Space-based MM is the area which requires most elaboration. Promising architectures for space manufacturing deserve closer examination. Furthermore, performance estimates have to be derived in terms that are useful for the extension of location theory into space.
Examination of MNT-based space transportation suggests a natural division of labor, with rotation deep-space tethers tending to operate further from the sun, and solar sails tending to operate closer to the sun.
Space manufacturing though MM requires more effort to adequately characterize. If that effort succeeds, all the parts should be available for an integrated examination of space manufacturing and space transportation, in a world of MNT.
The high performance estimates for MNT-based space systems suggest that its development would be quite sufficient to open up the tremendous resources beyond Earth. Even if not necessary, it should allow easier and fuller use of space's bounty.
Ultimately, an integrated examination of space manufacturing and transportation, using parameters appropriate for MNT, will give a much better planning estimate of what we will accomplish in space once we develop this promising technology. This avenue continues to deserve vigorous pursuit.
2 Soreff, Jeffrey, "Recent Progress: Steps Towards Nanotechnology," Foresight Update, No. 28, pp. 6-7, 10, March 30, 1997.
3 Saini, Subhash, "Petaflops Computing and Computational Nanotechnology," Nanotechnology, Vol. 7, No. 3, pp. 224-235, 1996.
4 McKendree, Thomas, "Educating Systems Engineers For an Impending Metatechnology in Product and Process Systems," Proceedings of the Third Annual Symposium of the National Council On Systems Engineering, James E. McAuley and William H. McCumber, ed., pp. 417-424, 1993.
5 Drexler, K. Eric, Engines of Creation. Anchor Press/Doubleday, Garden City, New York, 1986.
6 Drexler, K. Eric, "Nanotechnology and the Challenge of Space Development," Proceedings of the 1988 International Space Development Conference, 1988.
7 Drexler, K. Eric, "Molecular Manufacturing as a Path to Space," Prospects of Nanotechnology, Markus Krummenacker and James Lewis (eds.), John Wiley & Sons, 1995.
8 Bishop, Forrest F., "The Interworld Rapid Transit System," submitted to Journal of the British Interplanetary Society, (draft) 1996.
9 McKendree, Thomas L., "Implications of Molecular Nanotechnology Technical Performance Parameters on Previously Defined Space System Architectures," Nanotechnology, Vol. 7, No. 3, pp. 204-209, 1996.
10 Hurter, Arthur P., and Joseph S. Martinich, Facility Location and the Theory of Production, Kluwer Academic Publishers, 1989.
11 Boden, Daryl G., "Introduction to Astrodynamics," Space Mission Analysis and Design, Wertz, James R., and Wiley J. Larson (eds), Kluwer Academic Publishers, pp. 113-140, 1991.
12 Lewis, John S., Mining the Sky: Untold Riches from the Asteroids, Comets, and Planets, Addison-Wesley, 1996.
13 Drexler, K. Eric, "Molecular Manufacturing for Space Development: An Overview," Journal of the British Interplanetary Society, Vol. 45, pp. 401-405, 1992.
14 Drexler, K. Eric, Nanosystems: Molecular Machinery, Manufacturing, and Computation. John Wiley & Sons, New York, 1992.
15 Mackenzie, Bruce A., "Bootstrapping Space Communities with Micro Rovers and High Tensile Boot Laces (Tethers)," Space Manufacturing 10: Pathways to the High Frontier, Barbara Faughnan (ed.), AIAA, pp. 235-244, 1995.
16 Moravec, Hans, "A Non-Synchronous Orbital Skyhook," Journal Astronautical Science, Vol. 25, No. 4, pp. 307-322, 1977.
17 Rechtin, Eberhardt, Mark W. Maier, The Art of Systems Architecting, CRC Press, 1997.
18 Merkle, Ralph. C., "Self Replicating Systems and Molecular Nanotechnology," Journal of the British Interplanetary Society, Vol. 45, No. 10, pp. 407-413, 1992.
19 Merkle, Ralph. C., "Design Considerations for an Assembler," Nanotechnology, Vol. 7, No.3, pp. 210-215, 1996.
20 Freitas, Robert A., Jr., "A Self-Reproducing Interstellar Probe," Journal of the British Interplanetary Society, Vol. 33, pp. 251-264, 1980.
21 Freitas, Robert A., Jr., and William P. Gilbreath (Eds.), Advanced Automation for Space Missions, NASA CP-2255, 1982.
22 Maryniak, Gregg, "Self-Replicating Machines for Space," SSI, 1984
23 Reitz, G, R. Facius and H. Sandler, "Radiation Protection in Space," Acta Astronautica, Vol. 35, No. 4/5, pp. 313-338, 1995.
24 Johnson R D, Holbrow C, Space Settlements: A Design Study, NASA SP-413, 1977
25 Drexler, K. Eric, personal communications, 1995p.
26 Rechtin, E., Systems Architecting: Creating & Building Complex Systems, Prentice-Hall, 1991.
27 O'Neill, Gerard K., The High Frontier, Space Studies Institute Press, 1982.
28 Drexler, K. Eric, Peterson, Chris and Pergamit, Gayle, Unbounding the Future: The Nanotechnology Revolution. William Morrow & Company, New York, 1991.
29 Williamson, Ray A., "The Industrialization of Space: Prospects and Barriers," The Exploitation of Space, Michiel Schwartz and Paul Stares (eds.), Butterworth, 1985.
30 Bishop, Forrest F., "Open Air Space Habitats," Tools for the Next Millennium, Lance Chambers (ed.), CRC Press, (forthcoming).
31 McKendree, Thomas L., "Planning Scenarios for Space Development," Space Manufacturing 10: Pathways to the High Frontier, Barbara Faughnan (ed.), AIAA, pp. 254-264, 1995a.
32 Regis, Ed, Nano, Little, Brown & Company, 1995.
33 Cassenti, B.N., G.L. Matloff, and J. Strobl, "The Structural Response and Stability of Interstellar Solar Sails," Journal of the British Interplanetary Society, Vol. 49, pp. 345-350, 1996.